개발계발
검색 알고리즘 본문
선형 검색
가장 기본적인 알고리즘으로 직선으로 늘어선 배열에서 원하는 키 값을 가진 원소를 찾을 때까지 맨 앞부터 순서대로 검색하는 알고리즘이다.
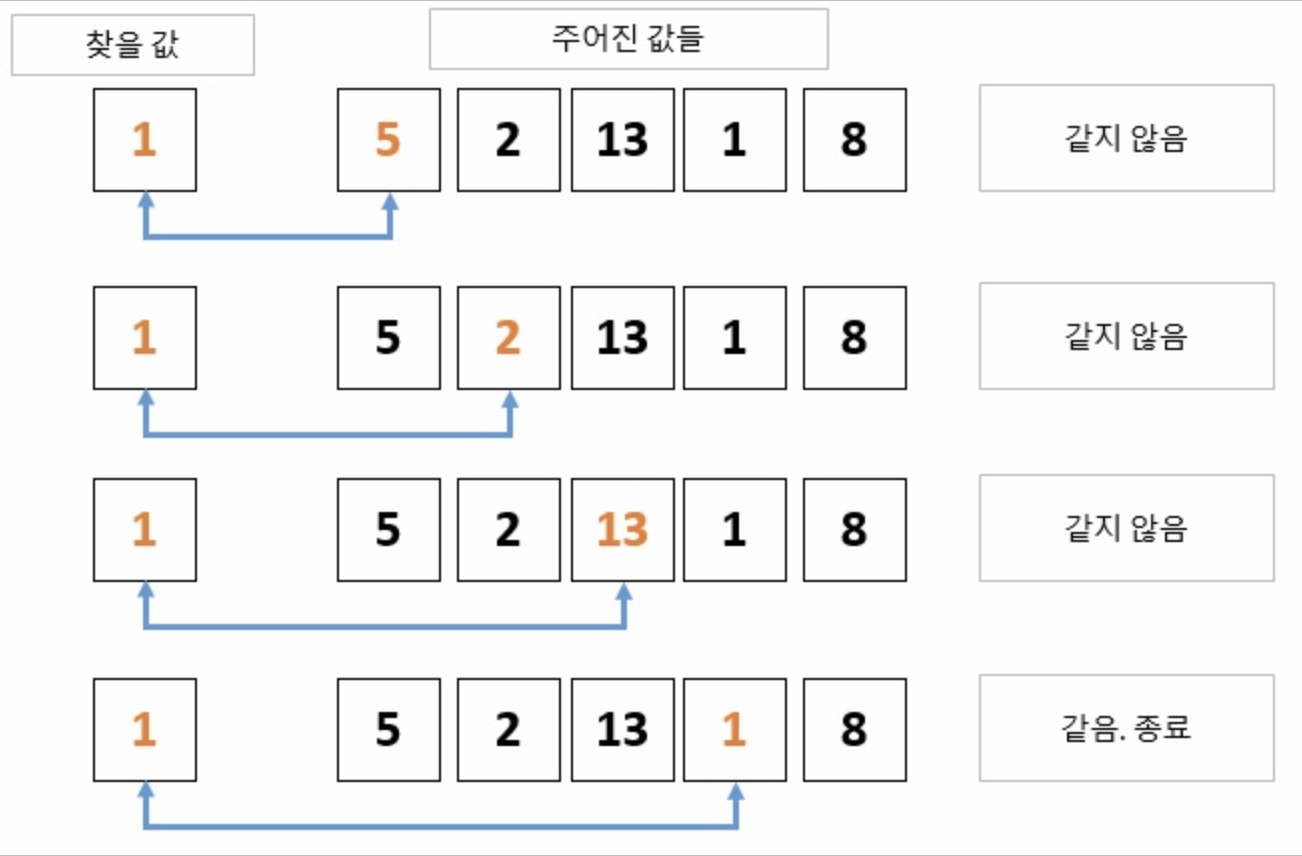
배열의 첫 원소부터 순차적으로 검사하기 때문에 시간 복잡도는 O(n)이다.
선형 검색 알고리즘을 코드로 구현하면 아래와 같다.
from typing import Any, Sequence
def seq_search(a: Sequence, key: Any) -> int:
i = 0
while True:
if i == len(a):
return 0
if a[i] == key:
return 1
i += 1하지만 위 코드에서 while문을 한 번 반복할 떄마다 2가지 종료조건(if문)을 체크하게된다.
이 비용을 줄이기 위한 방법으로 보초법을 사용할 수 있다.
보초법
검색할 값을 배열의 맨 끝에 추가함으로써 종료조건을 단순화해 비용을 줄이는 방법
예를 들어 위 그림에서 9라는 값을 찾는다고 생각해보자.
그럼 먼저 찾고자 하는 값을 배열의 끝에 임의로 추가해주고 코드를 아래와 같이 수정한다.
from typing import Any, Sequence
import copy
def seq_search(seq: Sequence, key: Any) -> int:
a = copy.deepcopy(seq)
a.append(key)
i = 0
while True:
if a[i] == key:
break
i += 1
return 0 if i == len(seq) else 1변경된 코드를 보면, 기존 코드에서 종료 조건을 확인하는 if문이 하나로 줄어든 것을 볼 수 있다.
즉, 비용이 1/2로 줄어든 것이다.(성능 개선)
위 코드에서 a값을 단순히 a = seq이 아닌 a = copy.deepcopy(seq)로 작성한 이유
a = seq는 단순 대입으로 a에는 seq가 가르키는 객체에 대한 새로운 참조가 저장되어, seq가 가리키는 객체를 변경하면 a도 같이 변경된다.
하지만, deepcopy를 사용하면 객체 전체의 복사본을 생성하기 때문에 원본 객체는 영향을 받지 않는다.
결론
변경된 코드가 시간복잡도 측면에서는 유리할 수 있으나, deepcopy로 추가 메모리를 사용하기 때문에 공간복잡도 측면에서는 불리할 수 있다.
이진 검색
이진 검색은 원소가 정렬된 배열에서 효율적으로 검색할 수 있는 알고리즘으로 시간복잡도는 O(log n)이다.
(정렬 알고리즘은 이후 포스팅에서 다룰 예정)

위 그림은 정렬된 배열에서 66을 찾는 과정이다.
배열의 중앙값과 찾고자 하는 값의 대소관계를 비교해 검색범위를 절반씩 줄여간다.
이를 코드로 구현하면 아래와 같다.
from typing import Any, Sequence
def bin_search(a: Sequence, key: Any) -> int:
pl = 0 # 검색 범위 맨 앞 원소의 인덱스
pr = len(a) - 1 # 검색 범위 맨 끝 원소의 인덱스
while True:
pc = (pl + pr) // 2 # 중앙 원소의 인덱스
if a[pc] == key:
return pc # 검색 성공(인덱스 반환)
elif a[pc] < key:
pl = pc + 1 # 검색 범위를 뒤쪽 절반으로 좁힘
else:
pr = pc - 1 # 검색 범위를 앞쪽 절반으로 좁힘
if pl > pr: # 검색범위가 역전됐을 경우(검색 실패)
break
return -1해시법
해시함수를 이용해 검색 뿐만 아니라 데이터 추가/삭제도 효율적으로 수행할 수 있는 방법
해시법을 쓰지 않은 정렬된 배열에서 원소를 추가할 경우에는 아래와 같이 다른 원소들의 위치를 모두 재조정해줘야한다.

결국 추가/삭제를 할 때 시간복잡도가 O(n)이 된다.
하지만, 해시법을 이용하면 이 비용을 평균 O(1)로 줄일 수 있다.
예를 들어, 해시 함수가 아래와 같을 때, (5/6/14/20/29/34/37/51/69/75)라는 값을 넣어보면
def hash_function(key):
hash_value = key % 13
return hash_value아래와 같은 결과가 나온다.
| 키 | 5 | 6 | 14 | 20 | 29 | 34 | 37 | 51 | 69 | 75 |
|---|---|---|---|---|---|---|---|---|---|---|
| 해시값 | 5 | 6 | 1 | 7 | 3 | 8 | 11 | 12 | 4 | 10 |
이렇게 나온 해시값을 통해 아래와 같이 해시테이블에 저장을 한다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | 14 | - | 29 | 69 | 5 | 6 | 20 | 34 | - | 75 | 37 | 51 |
그럼 이후에 '35'라는 값을 추가한다고 생각하면 35가 해시함수를 통해 나온 값이 9이기 때문에 9 인덱스에 저장해주면 된다.
즉, 검색, 추가, 삭제 모두 시간 복잡도가 O(n)이다.
--> 근데 그럼 같은 해시값이 나오면 어떻게 함??
이 경우를 해시 충돌이라고 하는데, 체이닝 기법 / 개방주소법 두 가지 해결법이 있다.
체이닝 기법
해시값이 같은 데이터를 연결 리스트로 연결하는 방법
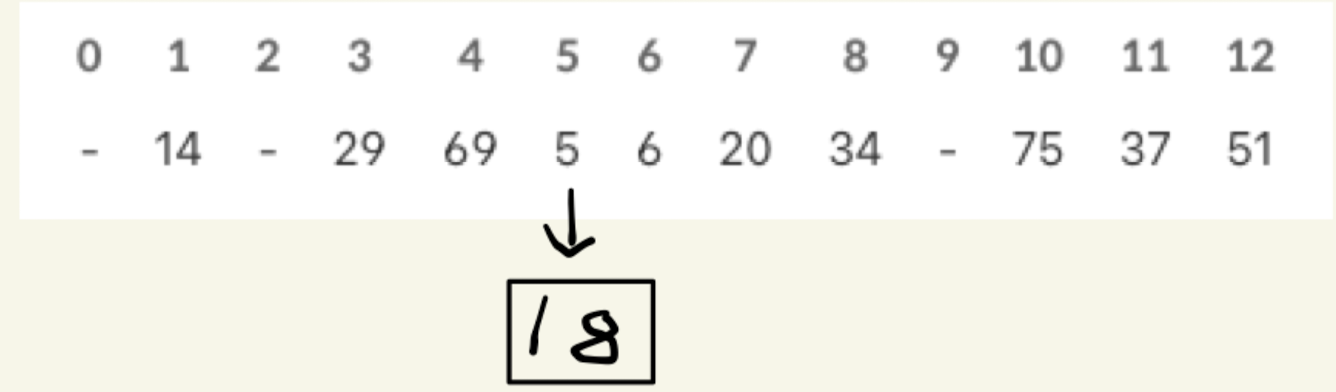
예를 들어, 위 표에서 18을 추가하려고 했을 경우 18을 13으로 나눈 나머지는 5이기 때문에 5번 인덱스 자리에 저장하려고 했지만 그 자리에는 이미 5가 저장돼있다.
이 경우, 5라는 값에 18을 연결시켜주는 것이다.
개방 주소법
재해시를 통해 빈 버킷을 찾아 저장하는 방법
해시함수를 통해 나온 해시값의 버킷에 이미 값이 저장됐을 경우, 재해시를 통해 다음 빈 버킷을 찾아 저장하는 방법이다.
그럼 여기서 의문이 들 수 있는데, 없는 값을 찾으려고 하면 끝까지 다 검사를 해봐야하는건가?
-> 재해시를 계속 수행하다가 빈 버킷을 만나면 검색에 실패한 것이다.
또 하나의 의문점 : 3번의 재해시를 통해 저장 후, 2번째 재해시를 한 위치의 값이 삭제됐을 경우는?
-> 이를 방지하기 위해, 삭제된 버킷의 경우 단순히 버킷을 비워두는 게 아니라 값이 삭제됐음을 표시해둔다.
즉, 2번째 재해시를 했는데, 해당 버킷이 삭제됐다라고 표시돼있을 경우 완전히 빈 버킷(삭제가 아니라 원래부터 빈 버킷)을 만날 때까지 재해시해본다.
'알고리즘' 카테고리의 다른 글
| 프로그래머스 - 분수의 덧셈(120808) (0) | 2024.04.23 |
|---|---|
| 프로그래머스 - 다항식 더하기(120863) (0) | 2024.04.23 |
| 프로그래머스 - 특이한 정렬(120880) (0) | 2024.04.23 |
| 프로그래머스 - 평행(120875) (0) | 2024.04.19 |
| 스택과 큐 (0) | 2024.03.28 |




